岩土力学与工程国家重点实验室最近提出了一种网格-无网格二象性数值模拟方法,为统一模拟连续、弱不连续、强不连续及其动态扩展问题提供了新思路。相关研究成果已发表在Theoretical and Applied Fracture Mechanics,Engineering Analysis with Boundary Elements以及《岩土力学》等国内外知名期刊上。
岩土力学与工程中的许多问题可以概化为连续、非连续及其扩展的组合问题,过去也被称为断续介质问题,典型地如干热岩及非常规能源开发中的水力压裂过程。在大量新型岩土工程需求的推动下,这一问题正在成为岩土工程数值分析的中心问题之一。目前已有大量基于有限元、有限体积(控制容积法或传统的积分-有限差分法)、边界元、离散元、无网格以及其组合的各种模拟方法,并取得了积极效果。但随着工程需求多样性和复杂性的不断提高,对于不同问题,各类方法仍然难以呈现一致的有效性,如表现为精度不足、网格依赖或者计算量过大等,从工程应用的角度,这一问题远未解决。
本研究中,研究人员首先基于偏微分方程的积分型求解路线提出了网格-无网格二象性思路,即将导数算子(未知函数及其导数)和积分算子的近似在对网格(拓扑)的使用上进行分离,即二者可分别采用网格或无网格方案,甚至可在计算过程中根据需要在网格和无网格之间切换。基于此,利用广义差分法逼近导数算子形成了用于连续部分的局部积分-广义差分离散格式(IGFD)。对于强非连续(已有裂缝及扩展裂缝)部分,则直接将其处理成子域边界,通过节点生死算法追踪裂纹扩展路径,新增节点自由度用已知节点自由度近似,可保持总体节点数及自由度不变,这些策略构成了扩展的IGFD(xIGFD)方法。算例和对比研究表明,该方法对连续问题显示出较高精度及收敛效果,边界条件处理简单,对裂缝及其扩展的模拟既不需要基于先验知识的富集函数,也无需重新剖分网格,体现了连续和非连续模拟的统一性和简洁性。因此,该方法在更复杂岩土工程问题的模拟中值得进一步研究探索。
本研究得到国家自然科学基金项目(No.41972316)以及四川省科技计划项目(No.2022YFSY0007)的资助。
论文链接:
https://www.sciencedirect.com/science/article/pii/S0955799722000650
https://www.sciencedirect.com/science/article/pii/S0167844223000514
http://ytlx.whrsm.ac.cn/CN/10.16285/j.rsm.2021.0559
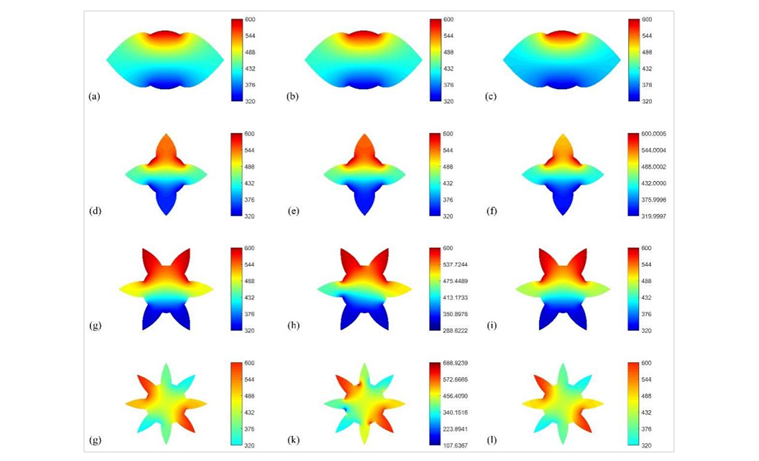
图1 在不同形状连续传热问题中的应用对比:积分-广义差分法IGFD(左)、广义差分法GFD(中)、有限元法FEM(右)
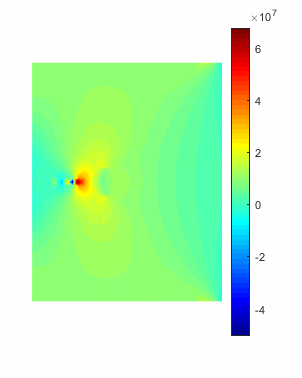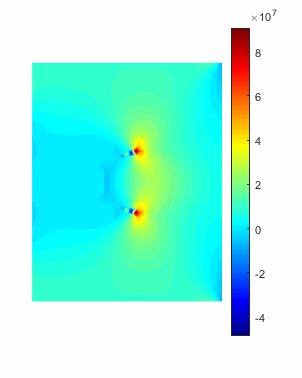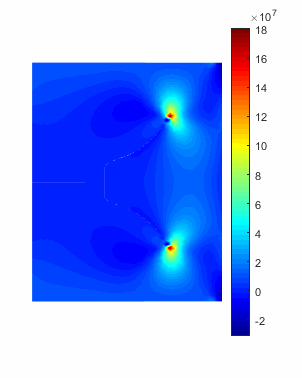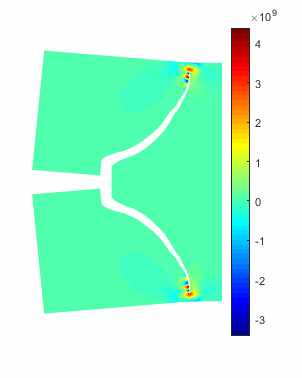
图2 T型裂纹扩展交叉过程
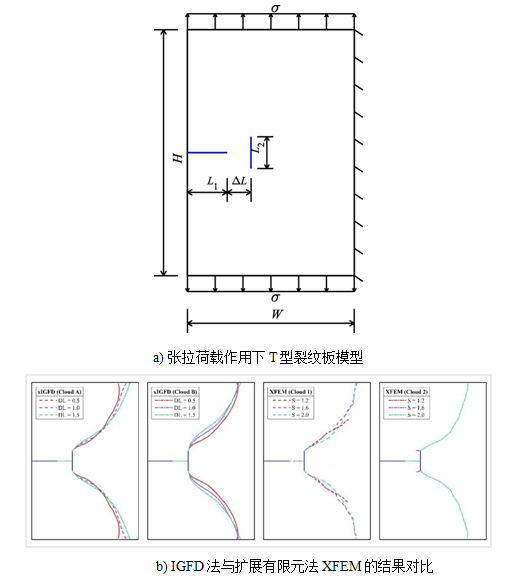
图3 T型裂纹扩展交叉模拟
 附件下载:
附件下载: